Théorème de Shannon

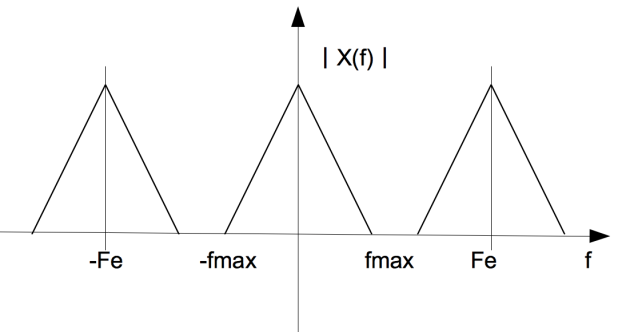
La condition nécessaire et suffisante pour échantillonner un signal sans perte d'information est que la fréquence d'échantillonnage Fe soit supérieure ou égale au double de la fréquence maximale du signal.

Plus précisément, si on note Fmax la fréquence maximale du signal, il faut et il suffit que fe ≥ 2fmax.

Si nous supposons que le signal s(t) possède un spectre borné tel que S(f)=0 si f n’appartient pas [−fmax, fmax], nous voyons que le spectre du signal échantillonné sera non recouvert si la condition fe ≥ 2fmax n’est pas vérifiée.

Par exemple, si l'on veut numériser le signal analogique qui possède une bande passante s'étendant entre 300 et 3400 Hz.
Quelle doit être la fréquence d'échantillonnage minimum ?
La formule du théorème de Shannon nous montre que la fréquence d'échantillonnage doit être supérieure au double de la fréquence maximum (3400Hz), soit 6 800 Hz.

Pourquoi cette propriété est importante ?

Si est trop faible, alors les répliques recouvrent le motif initial ce qui se traduit par une distorsion du spectre et par conséquent une perte irréversible d'information. C'est le cas de la figure ci-dessous.

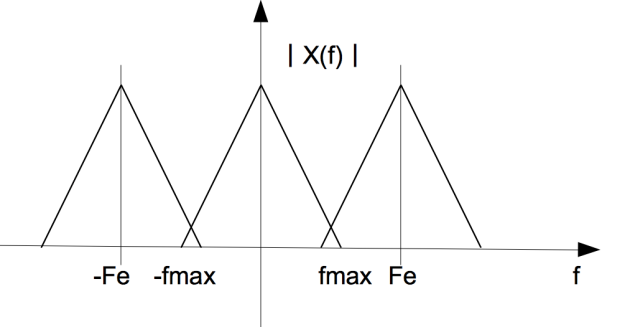
A cause du chevauchement des motifs constituant le spectre Xe(f) du signal échantillonné, il n'est pas possible de récupérer le spectre X(f) par un filtrage approprié. Il n'est donc pas possible de reconstruire le signal initial x(t) à partir de la connaissance de son échantillonné xe(t).